Lesson 3: Polygons and Parameters

In the first lesson, we taught the turtle how to draw a square. We ended up with a procedure that looks like this: 

TO SQUARE
  REPEAT 4 [ FORWARD 100 RIGHT 90 ]
END

In this lesson, we are going to improve upon this procedure. We are going to create a procedure that draws squares of any size. And we are going to create a procedure that draws other shapes.

Drawing Squares of Any Size

Our SQUARE procedure is pretty good, but we can make it better. Right now, the turtle only knows how to draw squares that are 100 pixels long on each side. Let's teach the turtle how to draw squares of any size.

We can do this by using something called a "parameter". A parameter is like a fill-in-the-blank for a procedure. When you define a procedure, you leave some values blank. When you call that procedure, you give it a value to use in that blank.

This may sound complicated, but it's not. In fact, you already know a procedure that takes a parameter: FORWARD. When you give the turtle a "FORWARD" instruction, you can't just say "FORWARD", you also have to tell him how many screen dots to move forward. This number is a parameter.

We are going to make SQUARE take a parameter that tells the turtle how long each side should be.

Activity: Press the "Edall" button and change the SQUARE function to the following: 

TO SQUARE :LENGTH
  REPEAT 4 [ FORWARD :LENGTH RIGHT 90 ]
END

The ":LENGTH" is our parameter. When we use this SQUARE procedure, we have to put a number after it. The number we use will be the number of pixels that the turtle moves forward when drawing each side. For example, "SQUARE 10" tells the turtle to make a square with sides that are 10 pixels long.

We can use our more powerful SQUARE procedure to draw an interesting design. 

REPEAT 10 [ SQUARE REPCOUNT * 10 ]
mutliple squares

Drawing a Polygon with any Number of Sides

Now the turtle can draw a square of any size, but what about other shapes. What about a triangle? What about a polygon with five sides? What about a polygon with a hundred sides? Can we make a single procedure that draws a polygon with any number of sides?

Let's look at some code for drawing polygons and try to find a pattern. 

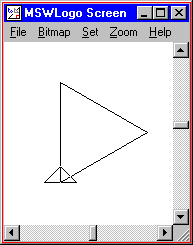
REPEAT 3 [ FORWARD 100 RIGHT 120 ]
a triangle 
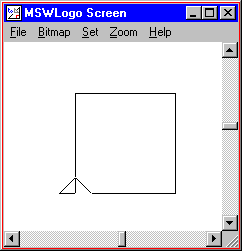
REPEAT 4 [ FORWARD 100 RIGHT 90 ]
a sqaure 
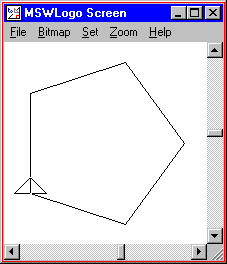
REPEAT 5 [ FORWARD 100 RIGHT 72 ]
a hexagon 
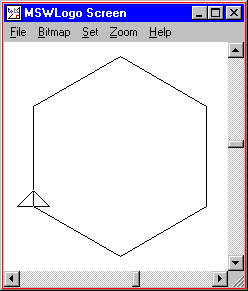
REPEAT 6 [ FORWARD 100 RIGHT 60 ]
a pentagon

Do you see a pattern? All of these shapes were drawn by repeatedly moving forward and turning right. The number of times we repeat equals the number of sides. The amount that we moved forward doesn't change. The amount we turn seems to get smaller with more sides.

Now for the hard part: how much should we turn? If you add up the "outside angles" of any closed polygon, you always get 360°. In the shapes that we have drawn, all angles are the same size. For example, in a triangle, we have three angles. Since we have to turn a total of 360° for all three angles put together, each angle should be 360° divided by 3, or 120°.

So let's create a procedure that can draw all of the shapes above. We'll call this procedure "POLYGON". By the way, in Logo you divide by using the "/" operator. 

TO POLYGON :SIDES
  REPEAT :SIDES [ FORWARD 100 RIGHT 360 / :SIDES ]
END


POLYGON 3
a triangle 
POLYGON 4
a square 
POLYGON 5
a hexagon 
POLYGON 6
a pentagon

Activity: Type in the POLYGON procedure and play around with it. What happens when you give it a number less than 3? What happens when you give it a large number, like 50?

Activity: Modify the POLYGON procedure to take a :LENGTH parameter, like we did for the SQUARE routine.

Activity: Create your own procedures that take a parameter. You can start from scratch or you can start with one of the samples from any lesson.

Sample Programs

TO RIGHTTRIANGLE :LENGTH
  FORWARD :LENGTH
  RIGHT   135
  FORWARD :LENGTH * SQRT 2
  RIGHT   135
  FORWARD :LENGTH
  RIGHT   90
END

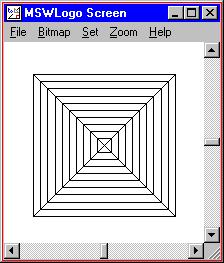
TO PYRAMID
  RIGHT 45
  REPEAT 4 [
    REPEAT 10 [ RIGHTTRIANGLE REPCOUNT * 10 ]
    RIGHT 90
  ]
  LEFT 45
END
 
PYRAMID
PYRAMID 
TO POLYGON :SIDES :LENGTH
  REPEAT :SIDES [
    FORWARD :LENGTH
    RIGHT 360 / :SIDES
  ]
END

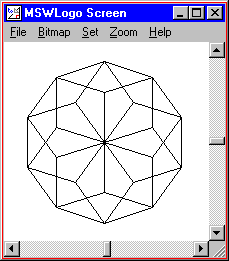
TO HEXAGONFLOWER :PETALS
  REPEAT :PETALS [
    POLYGON 5 50
    RIGHT 360 / :PETALS
  ]
END

HEXAGONFLOWER 10
HEXAGONFLOWER 10 
TO DOWNSLANT :LENGTH
  REPEAT 2 [
    FORWARD :LENGTH
    RIGHT   135
    FORWARD 20
    RIGHT   45
  ]
  RIGHT   135
  FORWARD 20
  LEFT    135
END

TO UPSLANT :LENGTH
  REPEAT 2 [
    FORWARD :LENGTH
    RIGHT   45
    FORWARD 20
    RIGHT   135
  ]
  RIGHT   45
  FORWARD 20
  LEFT    45
END
 
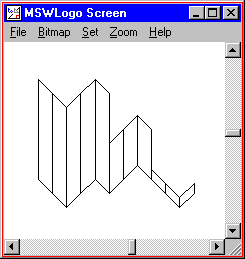
TO SHEET
  REPEAT 2 [ DOWNSLANT 100 ]
  REPEAT 2 [ UPSLANT   100 ]
  DOWNSLANT 100
  REPEAT 2 [ UPSLANT   50  ]
  DOWNSLANT 50
  REPEAT 2 [ DOWNSLANT 10  ]
  UPSLANT 10
END

SHEET
SHEET 
TO RECTANGLE :HEIGHT :WIDTH
  REPEAT 2 [
    FORWARD :HEIGHT
    RIGHT   90
    FORWARD :WIDTH
    RIGHT   90
  ]
END

TO TRIANGLE :LENGTH
  RIGHT 45
  FORWARD :LENGTH * (SQRT 2) / 2
  RIGHT 90
  FORWARD :LENGTH * (SQRT 2) / 2
  RIGHT 135
  FORWARD :LENGTH
  RIGHT 90
END

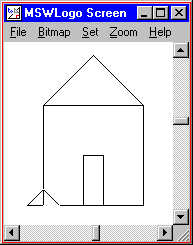
TO HOUSE
  ; draw the house
  RECTANGLE 100 100
 
  ; draw the roof
  FORWARD  100
  TRIANGLE 100
  BACK     100

  ; draw the door
  RIGHT     90
  FORWARD   60
  LEFT      180
  RECTANGLE 20 40
  FORWARD   60
  RIGHT     90
END

HOUSE
HOUSE 
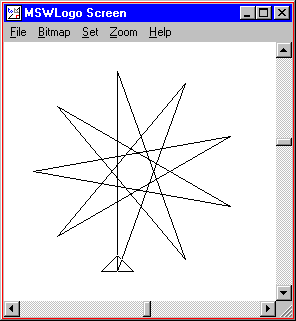
TO STAR :LENGTH :POINTS
  REPEAT :POINTS [
    FORWARD :LENGTH
    RIGHT   180 - (180 / :POINTS)
  ]
END

STAR 200 9
STAR 200 9 
TO TRIANGLE :LENGTH
  REPEAT 3 [FORWARD :LENGTH RIGHT 120 ]
END

TO TRIANGLEFLOWER :LENGTH :COUNT
  REPEAT :COUNT [ 
    TRIANGLE  :LENGTH
    RIGHT     360 / :COUNT
  ]
END

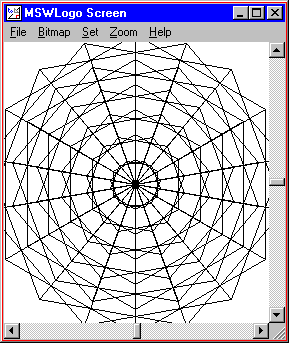
TO WEB
  REPEAT 6 [ TRIANGLEFLOWER REPCOUNT * 25 18 ]
END

WEB
WEB

Challenge Questions