Lesson 8: Fractals

Today we are going to cover fractals. Fractals are pictures that, when you look at a small area of the picture, it looks similar to the overall picture (and other small areas, too). This property is called "self-similar". Many things in nature can be drawn better with fractals than with simple polygons. For example, think about a pine tree. The main branch (or trunk) has smaller branches coming off it. Those branches have smaller branches coming off of it. And so on, until you get to the pine needles. That is sort of self-similarity is exactly what fractals are.

Fractals are surprisingly easy to draw in Logo.

Recursion

Before we can draw fractals, we must master a new programming technique called "recursion". Recursion is when a command calls itself. Recursive commands all follow the same pattern: they do a little work, then call themselves with simpler inputs. This, in turn, will do a little more work and call itself with even simpler inputs. When the input is so simple that there's essentially nothing to be done, the command just stops without doing any work (and without calling itself). Don't worry if you don't see why recursion is useful, that will become clear when we go through a few activities.

Anything you can do with a REPEAT loop can also be done with recursion. For example, let's take our routine for drawing a square from the first lesson. 

TO SQUARE
  REPEAT 4 [ FORWARD 100 RIGHT 90 ]
END

SQUARE

Now let's write a recursive version of it. 

TO SQUARE.RECURSIVE :SIDES.TO.GO
  ; base case: do nothing
  IF :SIDES.TO.GO = 0 [ STOP ]

  ; recursive case: draw a side and call recursively
  FORWARD 100
  RIGHT   90
  SQUARE.RECURSIVE :SIDES.TO.GO - 1
END

SQUARE.RECURSIVE 4

SQUARE.RECURSIVE inputs the number of sides of the square to draw. This seems a bit silly, since all squares have four sides, but it's part of how the recursion works.

Observe that there are two parts to the recursive function: the "base case" and the "recursive case". As SQUARE.RECURSIVE works, it uses the recursive case. The recursive case draws one side of the square, then calls SQUARE.RECURSIVE with an input that is one smaller than what it received. It's one smaller because the input represents the number of sides to draw and the command just drew one of them.

The "base case" is used when SQUARE.RECURSIVE should stop calling itself. This happens when there are no more sides left to be drawn, that is, when :SIDES.TO.GO is 0. Without the base case, Logo would draw the sides of a square forever.

Activity: Type in the SQUARE.RECURSIVE and call it.

Our First Fractal: Embedded Squares

Now let's use recursion to draw a fractal. We'll start with a square. We'll draw a smaller square in every corner of this square. In each of these smaller squares, we'll draw even smaller squares. And so on.

SQUARE.FRACTAL follows the pattern of RECURSIVE.SQUARE, but it recurses on a :DEPTH input, instead of :SIDES.TO.GO. :DEPTH represents the number of times the fractal is repeated. The base case is when :DEPTH = 0. The recursive case draws a square with a familiar REPEAT instruction. After drawing each side, it calls RECURSIVE.SQUARE to draw a smaller sqaure in each corner. 

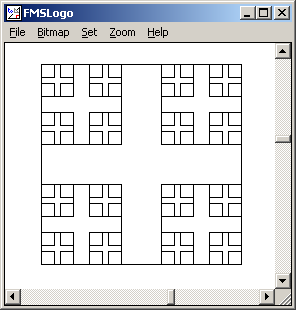
TO SQUARE.FRACTAL :LENGTH :DEPTH

  ; base case: no more squares
  IF :DEPTH = 0 [ STOP ]

  ; recursive case: draw a square such that each corner
  ; of the square has SQUARE.FRACTAL in it.
  REPEAT 4 [
    FORWARD :LENGTH
    RIGHT   90
    SQUARE.FRACTAL :LENGTH * 0.4 :DEPTH - 1 
  ]

END

SQUARE.FRACTAL 200 4
Square Fractal

Activity: Run SQUARE.FRACTAL. You may want to run SLOWDRAW 10 to see how the picture is drawn in slow motion.

Sample Programs

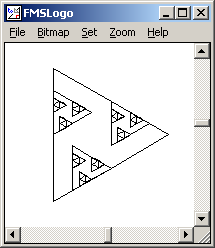
TO TRIANGLE.FRACTAL :LENGTH :DEPTH

  ; base case:
  ; just move forward, no more squares
  IF :DEPTH = 0 [
    FORWARD :LENGTH
    STOP
  ]

  ; recursive case:
  ; draw a triangle such that each side of
  ; the triangle has TRIANGLE.FRACTAL in it.
  REPEAT 3 [
      FORWARD :LENGTH / 3
      TRIANGLE.FRACTAL :LENGTH / 3 :DEPTH - 1
      FORWARD :LENGTH / 3

      RIGHT 120
  ]
END

TRIANGLE.FRACTAL 200 4
TRIANGLE.FRACTAL 200 4 
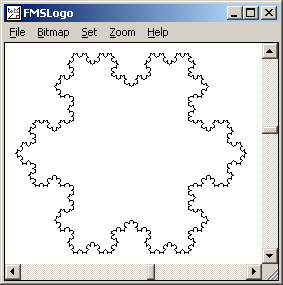
TO SNOWFLAKE.SIDE :LENGTH :DEPTH

  IF :DEPTH = 0 [
    FORWARD :LENGTH
    STOP 
  ]

  SNOWFLAKE.SIDE :LENGTH  / 3 :DEPTH - 1

  LEFT    60
  SNOWFLAKE.SIDE :LENGTH  / 3 :DEPTH - 1
  RIGHT   120
  SNOWFLAKE.SIDE :LENGTH  / 3 :DEPTH - 1
  LEFT    60

  SNOWFLAKE.SIDE :LENGTH  / 3 :DEPTH - 1
END

TO SNOWFLAKE :LENGTH :DEPTH
  REPEAT 3 [
    SNOWFLAKE.SIDE :LENGTH :DEPTH
    RIGHT 120
  ]
END
 
SNOWFLAKE 200 4
SNOWFLAKE 200 4 
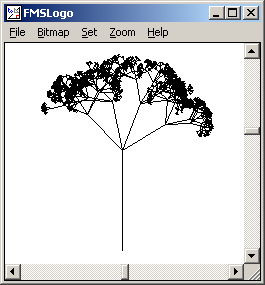
TO PLANT :SIZE :ANGLE
   IF :SIZE < 1 [ STOP ] 

   RIGHT :ANGLE
   FORWARD :SIZE
   REPEAT 4 [
     PLANT :SIZE / 2 DIFFERENCE RANDOM 160 80
   ]
   BACK :SIZE
   LEFT :ANGLE
END
 
PLANT 100 0
PLANT 100 0 
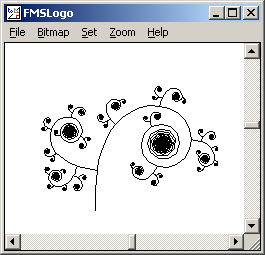
TO CURLY.FRACTAL :SIZE

  IF :SIZE < 0.5 [ STOP ]

  REPEAT 360 [

      IF REPCOUNT = 5 [ 
         LEFT 90
         CURLY.FRACTAL :SIZE / 2
         RIGHT 90
      ]

      IF REPCOUNT = 10 [ 
         LEFT 90
         CURLY.FRACTAL :SIZE / 5
         RIGHT 90
      ]

      IF REPCOUNT = 15 [ 
         LEFT 90
         CURLY.FRACTAL :SIZE / 5
         RIGHT 90
      ]

      IF REPCOUNT = 20 [ 
         LEFT 90
         CURLY.FRACTAL :SIZE / 4
         RIGHT 90
      ]

      IF REPCOUNT = 25 [ 
         LEFT 90
         CURLY.FRACTAL :SIZE / 5
         RIGHT 90
      ]

      IF REPCOUNT = 30 [ 
         LEFT 90
         CURLY.FRACTAL :SIZE / 8
         RIGHT 90
      ]

      FORWARD :SIZE
      RIGHT REPCOUNT 
  ]

  RIGHT 180

END

CURLY.FRACTAL 10
CURLY.FRACTAL 10 
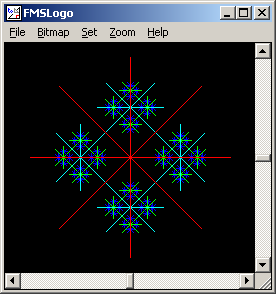
TO CRISSCROSS :SIZE :DEPTH
  IF :DEPTH = 0 [ STOP ]
  SETPENCOLOR :DEPTH
  REPEAT 4 [
    FORWARD :SIZE / 2
    CRISSCROSS :SIZE / 3 :DEPTH - 1
    FORWARD :SIZE / 2

    BACK :SIZE

    RIGHT 45
    FORWARD  :SIZE
    BACK :SIZE
    RIGHT 45
  ]
  SETPENCOLOR :DEPTH + 1
END

TO CRISSCROSSPICTURE
  SETSCREENCOLOR 0
  CRISSCROSS 100 4
END

CRISSCROSSPICTURE
CRISSCROSSPICTURE

Online Resources

For an in-depth look at several different fractals in Logo, check out Vladimir Batagelj's essay entitled Drawing space-filling curves in logo.

Challenge Questions