Lesson 2: Basic Loops

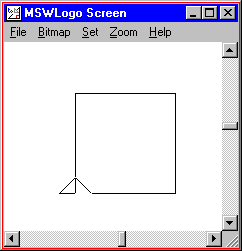
In the first lesson, we used a command called "REPEAT" to draw a square one side at a time. In this lesson, we will use more advanced features of the REPEAT command to draw pictures that are much more interesting.

The REPEAT Loop

In Logo, a "loop" is something that the computer does many times over. Loops are useful when you want to draw something that has several parts, all of which look the same. For example, we can draw a square by "looping" the command "FORWARD 100 RIGHT 90" four times, as in: 

REPEAT 4 [ FORWARD 100 RIGHT 90 ]
a sqaure

While loops are useful when a problem has parts that look exactly the same, the real fun starts when loops are used to draw pictures with parts that look similar, but are NOT exactly the same. For example, to draw a square spiral, you can start at the center and repeatedly draw the edges of a square, making each edge a little longer than the previous one. You do this in Logo with the "REPCOUNT" loop counter. REPCOUNT is always equal to the number of times the loop has been run. It is 1 the first time the loop is run, 2 on the second, 3 on the third, and so on.

Here is a program that uses REPCOUNT to draw a square spiral. 

REPEAT 100 [ FORWARD REPCOUNT * 2 RIGHT 90 ]
square spiral

Activity:

  1. Type in the square spiral program and run it.
  2. Modify the program to draw a triangle spiral.
  3. Pick some other number for the angle and see what happens.
  4. The square spiral multiplied the "FORWARD" amount by 2. What do you think happens if you change the "2" to a "3"? Try it and see if you're right.

Number Sequences

Have you ever heard NASA count backwards just before they launch a space shuttle? It goes something like this: "10, 9, 8, 7, 6, 5, 4, 3, 2, 1, BLASTOFF". They call this a "countdown sequence". The thing that makes it a "sequence" is that the order of the numbers is important. "9, 5, 1, 3, 6, 10, 8, 7, 3, 2" is NOT a countdown sequence, even though it has all the same numbers.

The square spiral procedure multiples "REPCOUNT" by 2. This turns the sequence <1, 2, 3, 4, 5,...> into <2, 4, 6, 8, 10, ...>. You can do a little math to turn the <1, 2, 3, 4, 5, ...> sequence into any other sequence that you want. For example, to get NASA's countdown sequence you could use "11 - REPCOUNT", as in: 

REPEAT 10 [ PRINT 11 - REPCOUNT ]
PRINT "BLASTOFF

Can you figure out how to get the sequence of numbers from 10 to 20? How about all odd numbers from 1 to 19? How about multiples of 7 between 14 and 77?

Activity: Experiment with REPEAT and REPCOUNT to create your own interesting pictures. You can start with any sample program that uses REPEAT and modify the loop to use "REPCOUNT" or you can write your own from scratch.

Sample Programs

TO STARSPIRAL
  REPEAT 45 [ FORWARD REPCOUNT * 5 RIGHT 144 ]
END
  
STARSPIRAL
STARSPIRAL 
TO SQUIRAL
  REPEAT 100 [ FORWARD REPCOUNT * 2 RIGHT 91 ]
END
  
SQUIRAL
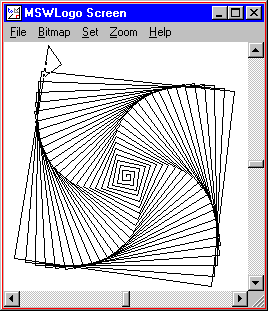
SQUIRAL 
TO EXPLOSION
  REPEAT 120 [ FORWARD REPCOUNT * 2 RIGHT 204 ]
END

EXPLOSION
EXPLOSION 
TO PATTERN
  REPEAT 22 [
    RIGHT 90
    FORWARD 110 - REPCOUNT * 10
    RIGHT 90
    FORWARD REPCOUNT * 10
  ]
END

PATTERN
PATTERN 
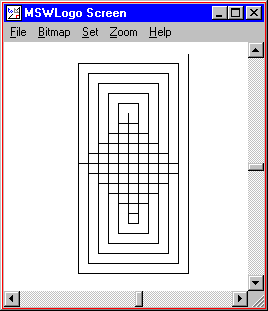
TO SSHAPE
  REPEAT 750 [
    RIGHT 90
    REPEAT 4 [ FORWARD REPCOUNT * 3 RIGHT 72 ]
    RIGHT REPCOUNT
  ]
END

SSHAPE
SSHAPE

Challenge Questions